1 Motivation (non-normative)

To effectively exchange business reporting information between a producing and a consuming application often requires the applications to perform validation on data types and values, apply consistency checks, test data quality, augment the data with calculated values and possibly corrections, and to provide feedback to the producing application that indicates the nature and severity of problems encountered. A producing application may also add calculated values and perform tests on its own outputs before sending results to consuming applications. Applications based on the exchange of spreadsheets that contain both data and formulas are common but present maintenance problems; here the intent is explicitly to separate the representation and location of formulas and validation criteria from a given instance.

These different functions are characteristic of many XBRL-enabled applications. That is because it is a goal of XBRL to allow applications to consume XBRL formatted business information no matter what its original source. Data entry validation (e.g., prohibiting dates such as February 31, 2001 from entering the system) is a familiar example of using a formula to flag errors, but the breadth and scope of formulas is much broader than this. Good information management practice generally recognizes that validations should be tested, adhered to, and corrections made as far “upstream” in an information supply chain as possible – recognizing, of course, that the same tests may be applied repeatedly as data makes its way from its many possible origins, to its many ultimate destinations.

Any general programming language could be used to perform computations on business data. However, there is regularity in business reporting information: regularity that is encoded in XBRL in instance constructs such as “facts,” “periods,” “entities,” and in taxonomies as items, definitions, and other relationships. Furthermore, applications that consume XBRL formatted data should be able to “publish the formulas” that govern documents containing XBRL data, so that producing applications can test and apply those formulas and thereby reduce delay, rework and retransmissions, and smooth and accelerate the flow of business reporting information.

Rule languages—in which rules are expressed as patterns to be matched and actions to be taken when the data matches the pattern—have a rich tradition and are nearly as old as computer science itself ([Newell, 1962]). They enjoyed a heyday in the 1980’s for the programming of “expert systems”, and today rule languages live on in languages such as Prolog, and in commercial products such as the Blaze Rule Engine [HNC] and JRules [ILOG]. Rule languages tend to be fairly compact and concise and resemble a database of logical sentences (“all people are mortal” “if X is a mountain, then the elevation of X must be positive”). They declare the rules to be obeyed, and an interpreter (or compiler) is responsible for efficiently executing the rules (matching patterns and executing actions) correctly when presented with incoming data.

Even if the goal of synthesizing information is set aside so as to merely detect violation of constraints, XML Schema [XSDL] itself is still not sufficient to this task because it allows the validation of individual data elements (“Revenues are a 12-digit nonnegative number”) and structural relationships (e.g., “an invoice must contain a header, a list of items, and an amount”) but does not express constraints between elements, also known as co-constraints (“if more than 10 dependents are claimed then Schedule K must be completed”). Besides, the nature of rules is that they generally compute a whole series of results, some of which may be considered fatal errors, others as warnings, others as merely informational; an XML Schema validator mainly detects fatal errors. Other general programming languages, including XML Schema Transformation [XSLT], could be pressed into service since they have the requisite pattern-action structure, but these neither take any account nor take any advantage of the constrained nature of XBRL instances, taxonomies, and so on.

XBRL-specific formulas are well motivated. The language would be, like XBRL itself, suitable for publishing and transporting between applications; it would exploit the XBRL language itself, and provide a concise and well constrained way of expressing common rules such as “Net Receivables cannot be negative,” “Net revenues are the difference between Gross revenues and Gross expenses,” “Unless income for the previous quarter was zero, income growth for the quarter is the ratio of the change in income between the current and previous quarter, divided by the income of the previous quarter,” and so on. The earliest discussions of XBRL acknowledged the need to express not only specific numeric facts (“1988 Revenue for TLA Inc. was $40m”), but also relationships among those facts (“TLA Inc. revenue consists of TBD Inc. revenue plus BFD Ltd. revenue less eliminations”) and general relationships (“The write down allowance for an asset in any year after 1993 is limited to 25% of its original purchase price”). There has now been sufficient experimentation and implementation experience with XBRL for the exchange of business reporting information in live and planned applications to have illustrated both the need for an extension to the language to meet this need, as well as illustrating deficiencies in schemes used to date and the typical patterns of usage and the limitations on what that language actually needs to cover. This information is advantageous to have because it limits the scope and guides the design of the language.

1.1 Terminology and formatting conventions

Terminology used in XBRL frequently overlaps with terminology from other fields. The terminology used in this document is summarised in Table 1.

Table 1: Terminology

abstract element, bind, concept, concrete element, context, Discoverable Taxonomy Set (DTS), duplicate items, duplicate tuples, element, entity, equal, essence concept, fact, instance, item, least common ancestor, linkbase, period, taxonomy, tuple, unit, taxonomy schema, child, parent, sibling, grandparent, uncle, ancestor, XBRL instance, c-equal, p-equal, s-equal, u-equal, v-equal, x-equal, minimally conforming XBRL processor, fully conforming XBRL processor.

As defined in [XBRL].

must, must not, required, shall, shall not, should, should not, may, optional

See [RFC2119] for definitions of these and other terms. These include, in particular:

SHOULD	Conforming documents and applications are encouraged to behave as described.
MUST	Conforming documents and consuming applications are required to behave as described; otherwise they are in error.

expression

An expression using constants, variables, arithmetic, logical, and functional operators.

formula

An expression along with criteria that indicate the domain of each variable in that expression and how they are to be bound.

rule

The term “rule” is not used in this version of the requirement, although it appeared previously as a synonym for “formula”.

variable

A “variable” appears in expressions as a symbol that the application of a formula binds to a value, so that the expressions of that formula can be evaluated.

argument

An “argument” of a formula is a formal parameter bound to some portion of an input instance. Some of the arguments will be identified as variables to be used in expressions.

The following highlighting is used for positive examples:

Example 1: Example of an example

Counterexamples indicate incorrect or unsupported examples:

Example 2: Example of a counterexample

Non-normative editorial comments are denoted as follows and removed from final recommendations:

WcH: This highlighting indicates editorial comments about the current draft, prefixed by the editor’s initials.

Italics are used for rhetorical emphasis only and do not convey any special normative meaning.

Distinctively bracketed and coloured numbers {1.2.3} refer to that particular numbered section of the XBRL 2.1 Specification Recommendation [XBRL].

1.2 Normative status

This document is normative in the sense that any formula specification recommendations by XBRL International MUST satisfy the requirements as they are stated here.

This document version depends upon XBRL 2.1 Specification Recommendation [XBRL].

XBRL Specification 2.1 does not depend in any way upon this document.

1.3 Language independence

The official language of XBRL International’s own work products is English and the preferred spelling convention is UK English. Unless otherwise stated, XBRL specifications must not require XBRL users to use English in documentation, item, tuple, entity, scenario or any other elements.

2 Use cases

The general use case for an XBRL formula specification is the externalisation and publication of a set of formulas that will be applied by a consuming application:

· A financial regulator collecting quarterly balance sheets and income statements;

· A statistical agency collecting market valuations of various asset categories;

· A tax authority accepting electronic tax filings;

· A stock exchange accepting registration requests;

· A bank evaluating loan applications or checking loan covenants;

More specifically, there are general use cases that these consuming applications may have:

1. Test XBRL instances for consistency and signalling the failure of a formula, in the same sense that an inconsistent set of fact bindings for the summation-item arcs of a calculation linkbase signals an inconsistency.

2. Test XBRL instances for consistency and provide detailed messages for each formula that failed. In this case, general XML output for further processing and rendering as appropriate by an application is likely to be sufficient.

3. Creating a tuple-free XBRL instance based on existing XBRL instances. In this case, it is sensible for a formula processor to produce a valid XBRL instance. If producing applications verify that their own output will be accepted by those consuming applications, significant efficiencies are possible, particularly in a distributed environment such as the Internet.

4. Transforming, adjusting, or composing XBRL instances. By contrast with use case 3 in which fact order is not relevant, element order can be significant in tuples.

Use case 4 encompasses use case 3, which encompasses use case 2, which encompasses use case 1.

The examples are expressed as “consistent” and “inconsistent” fact sets for use cases 1 and 2, and as “before” and “after” fact sets and instances for use cases 3 and 4, along with a structured description of the relevant generalisation of the behaviour illustrated by that case.

The examples shown in the requirements all depend on a single taxonomy shown in Figure 1 consisting mainly of financial position and performance items.

Figure 1: Items Appearing in Examples

@name	@type	@periodType	Label (en, standard)
Assets	monetaryItemType	instant	Assets
CurrentAssets	monetaryItemType	instant	Current Assets
FixedAssets	monetaryItemType	instant	Fixed Assets
Equity	monetaryItemType	instant	Equity
Shares	sharesItemType	instant	Shares
Price	monetaryItemType	instant	Price
Earnings	monetaryItemType	duration	Earnings
AvgShares	sharesItemType	duration	Average Shares
PE	pureItemType	instant	Price-Earnings Ratio
ROE	pureItemType	instant	Return on Equity
EPS	decimalItemType	duration	Earnings per Share
AssetsEquity	pureItemType	instant	Assets-to-Equity Ratio
Rating	integerItemType	instant	Rating
AssetsOkay	booleanItemType	instant	Assets Okay
EquityOkay	booleanItemType	instant	Equity Okay
AssetsMessage	stringItemType	instant	Assets Message
AssetsLB	booleanItemType	instant	Assets in Lower Bound
AssetsUB	booleanItemType	instant	Assets in Upper Bound
AssetsLarge	booleanItemType	instant	Assets not too Large
AssetsSmall	booleanItemType	instant	Assets not too Small
IntangiblesPatents	monetaryItemType	instant	Intangibles (Patents)
IntangiblesClass	stringItemType	instant	Intangibles Class
IntangibleGross	monetaryItemType	instant	Intangible Gross
IntangibleReserve	monetaryItemType	instant	Intangible Reserve
IntangibleNet	monetaryItemType	instant	Intangible Net
IntangibleAsset	tupleType		Intangible Asset
AutoWriteDown	tupleType		Automobile Write-Down
AutoName	tokenItemType	duration	Automobile Name
AcquisitionDate	dateItemType	duration	Acquisition Date
WriteDownAllowance	monetaryItemType	duration	Write-Down Allowance
WDVBroughtForward	monetaryItemType	duration	Write-Down Value Brought Forward
UsefulLife	durationItemType	duration	Useful Life

All facts in the examples have a unitRef and contextRef drawn from the units and contexts shown in Figure 2 and Figure 4, respectively. The namespace prefix si refers to international standard scientific units.

Figure 2: Units Appearing in Examples

@id	measure
usd	iso4217:USD
gbp	iso4217:GBP
pure	xbrli:pure
shs	xbrli:shares
usdsh	iso4217:USD/xbrli:shares
gbpsh	iso4217:GBP/xbrli:shares
year	si:year

The namespace prefix co with elements aaa and bbb are used to distinguish segments of entity 444. The elements actual, budgeted and variance are used to distinguish scenarios.

Figure 3: Segments and Scenarios Appearing in Examples

prefix	element
co:	<aaa/>
co:	<bbb/>
co:	<actual/>
co:	<budgeted/>
co:	<variance/>

Figure 4: Contexts Appearing in Examples

@id	entity/ @identifier	entity/ segment	period/ instant	period/ startDate	period/ endDate	scenario
c01	333			2003-01-01	2003-12-31
c02	333		2002-12-31
c03	333		2003-12-31
c04	444			2003-01-01	2003-12-31
c05	444		2003-12-31
c06	333		2003-12-31
c07	444	<geo>ON</geo>		2003-01-01	2003-12-31
c08	444	<geo>ON</geo>	2003-12-31
c09	444	<geo>MI</geo>		2003-01-01	2003-12-31
c10	444	<geo>MI</geo>	2003-12-31
c11	444		2003-12-31			<co:actual/>
c12	444		2003-12-31			<co:budgeted/>
c13	444		2003-12-31			<co:variance/>
c14	444			1993-01-01	1993-12-31
c15	444			1995-01-01	1995-12-31
c16	333		2001-12-31
c17	444	<lob>paper</lob>		2003-01-01	2003-12-31
c18	444	<lob>paper</lob>	2003-12-31
c19	444	<lob>plastic</lob>		2003-01-01	2003-12-31
c20	444	<lob>plastic</lob>	2003-12-31

Note that contexts c06 and c03 are s-equal.

The data type of the content in any UsefulLife fact is assumed to be yearMonthDuration; the XBRL durationItemType does not specify whether fact content is yearMonthDuration or dayTimeDuration.

Each fact in this document also has a unique identifier such as f42; the identifiers are not relevant in any way to processing the facts or formulas, but the identifiers allow them to be referred to in the text.

Expressions are written in XML Path Language 2.0 [XPATH2] and are meant to be transparent for the example at hand, but are not prescriptive as to the expression language to be required. Some cases use the syntax of XML Query Language 1.0 [XQuery] to declare functions; as stated in [XPATH2], “XPath is designed to be embedded in a host language such as XSLT 2.0 or XQuery… XPath per se does not provide a way to declare functions, but a host language may provide such a mechanism.” The host language chosen in the examples is XQuery because it allows users to declare functions of their own.

3 Linkbase-related requirements

The requirements here specify the linkbase features that formulas must support in order to integrate fully with the rest of XBRL.

All these requirements are common to all four use cases.

3.1 A discoverable taxonomy set may include formulas

It must be possible to define a set of formulas in such a way that it can be part of one or more discoverable taxonomy sets {1.4}.

3.2 Formulas may require components of a DTS

Formulas refer to items and tuples defined in taxonomies {3}. Therefore it must be possible for a set of formulas to rely upon the presences of specific taxonomy schemas and linkbases in its processing environment.

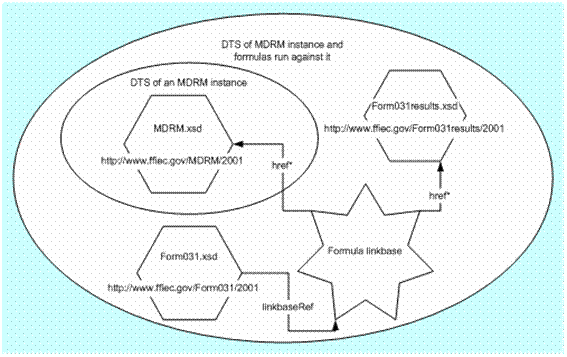
It is not sufficient to rely on the schemaRef and linkbaseRef elements of an instance because the formulas may be computing results that are elements from an entirely different taxonomy schema. Example 3 shows a formula linkbase that has inputs from the taxonomy schema MDRM.xsd but computes results that are items in Form031results.xsd. An instance with a schemaRef only to MDRM.xsd is not sufficient for execution of the formulas. In effect the execution of formulas requires a DTS that is the union of its own DTS and the DTS of the instance in question.

Example 3: Relationship of an instance DTS and DTS of a set of formulas

3.3 Formulas may be partitioned into sets

Formulas maintained in the same taxonomy may provide alternative, possibly incompatible definitions for the same item. A formula is a relationship among two or more facts and so a set of formulas must use the same xlink:role attribute as used in XBRL to indicate which relationships participate in the same networks of relationships based on the value of the role {5.2}.

Example 4: Incompatible formulas are distinguishable.

EPS for some purposes is computed using the average number of shares during the earnings period, and for other purposes using the number of shares at the end of the period.

Formulas:

item	test	expression	type	matching
EPS	“method 1”	($Earnings div $AvgShares)	decimals=7	p-equal, c-equal.
EPS	“method 2”	($Earnings div $Shares)	decimals=7	p-equal; Shares context period/instant = Earnings context period/endDate.

item

test

expression

type

matching

EPS

“method 1”

($Earnings div $AvgShares)

decimals=7

p-equal, c-equal.

EPS

“method 2”

($Earnings div $Shares)

decimals=7

p-equal;

Shares context period/instant =

Earnings context period/endDate.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000
f29	EPS	c01	usdsh	INF	0.2

Inconsistent Facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000
f82	EPS	c01	usdsh	9	-.183333333

Use cases 3 and 4:

Initial facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000
f17	Shares	c03	shs	INF	60000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f29	EPS	c01	usdsh	INF	0.2
f67	EPS	c01	usdsh	9	0.183333333

In this example, only one of the two results should be computed, depending on whether the (set of) formulas labelled “method 1” or “method 2” is selected for processing. The xlink:role attribute may be an appropriate way to model this, since the evaluation of the condition does not depend in any way on the facts in the instance.

3.4 Formulas MAY be prohibited

An extension taxonomy MAY prohibit a formula in a base taxonomy {3.5.3.9.7.5}. The requirement does imply that formulas require a base/extension scheme like that used in taxonomies.

In order for one formula to prohibit another they must be identical, not just s-equal. Assuming that a formula set is implemented as a linkbase, a prohibiting arc MUST connect the same XML fragments as the original arc, and both the original and the prohibiting arc MAY connect multiple resources (formulas, variables, constants) by making the ID attribute required.

Example 5: Prohibiting a formula.

An extension {3.2} {3.5.3.9.7.5} of a set of formulas may need to change the method by which an item is computed in a base set of formulas. In this example, the simpler calculation of EPS is in the base set of formulas:

Formulas:

item	test	expression	type	matching
EPS		($Earnings div $Shares)	decimals=7	p-equal; Shares context period/instant = Earnings context period/endDate.

item

test

expression

type

matching

EPS

($Earnings div $Shares)

decimals=7

p-equal;

Shares context period/instant =

Earnings context period/endDate.

An extension set of formulas then prohibits that formula, and asserts a different one:

Formulas:

item	test	expression	type	matching
~~EPS~~		~~($Earnings div $Shares)~~	~~decimals=7~~	~~p-equal;~~ ~~Shares context period/instant =~~ ~~Earnings context period/endDate.~~
EPS		($Earnings div $AvgShares)	decimals=7	p-equal, c-equal.

item

test

expression

type

matching

~~EPS~~

~~($Earnings div $Shares)~~

~~decimals=7~~

~~p-equal;~~

~~Shares context period/instant =~~

~~Earnings context period/endDate.~~

EPS

($Earnings div $AvgShares)

decimals=7

p-equal, c-equal.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000
f17	Shares	c03	shs	INF	60000
f29	EPS	c01	usdsh	INF	0.2

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000
f17	Shares	c03	shs	INF	60000
f83	EPS	c01	usdsh	9	.1833333333

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000
f17	Shares	c03	shs	INF	60000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f29	EPS	c01	usdsh	INF	0.2

In this example, the computation based on average number of shares is used and only one value of EPS is calculated.

3.5 Documentation of a formula may be included

Human-readable documentation that explains meaning of a formula in multiple languages may be included in each formula or set of formulas.

3.6 The representation of formulas should not require redundancy

This is a general principle applicable to most if not all representations. By analogy with the unit element in XBRL and the unitRef attribute, where a set of formulas is likely to share common information, the specification will use syntax that allows it to be specified just once and referred to in many formulas.

3.7 Formulas must only appear in linkbases associated with a taxonomy, consistent with the treatment of calculations, and not the instance.

Formulas in an instance are believed to irrevocably render XBRL instances useless from an archival standpoint because of differences in the results that different processors would derive results. The treatment of formulas for archiving must be the same as for calculation arcs.

4 Processing-related Requirements

The requirements here describe the processing semantics of formulas relative to input XBRL instances and outputs.

4.1 The result of applying formulas to an instance that is not XBRL-valid is not defined.

Authors may write formulas in such a way as to presume an XBRL-valid instance with respect to a known taxonomy schema.

This requirement is common to use cases 1, 2, 3, and 4.

4.2 Application of a set of formulas to an XBRL-valid instance MUST either fail or result in a well-formed XML instance.

One and only one processing iteration shall be performed in satisfying this requirement.

This requirement is common to use cases 1, 2, 3, and 4.

4.3 Application of a set of formulas to an XBRL-valid instance MUST either fail or result in another XBRL-valid instance.

Non-local properties of XBRL validity that would apply to the output instance—such as the testing of the requires‑element constraints {5.2.6.2.4}—can be difficult to guarantee on a local, incremental basis, so that in practice a formula processor would almost certainly require an XBRL validity checker.

One and only one processing iteration shall be performed in satisfying this requirement.

This requirement is common to use cases 3 and 4.

4.4 Any number of formulas may compute the value of any item.

Authors may write formulas in such a way as to provide multiple ways to derive a given fact. In practice authors should avoid writing formulas that bind the same set of facts to produce the same result facts, since the result facts may be duplicates or even contradictory.

This requirement is common to use cases 3 and 4.

4.5 All formulas in a DTS must be processed concurrently and without exception without regard to priority.

This requirement is common to use cases 1, 2 and 3, and does not apply to use case 4.

The firing order of formulas is implementation dependent. This cannot affect the semantics of the outcome, given requirement 6.7 below, “Formulas MUST only bind facts that are explicitly present in the input”

Formulas are to be processed one instance at a time. Processing the instances is implementation dependent and cannot affect the semantics of the outcome. There is no dependency between any formula and any other formula.

If formulas had priorities then they could be used to order formula application in cases where more than one formula applies, but since all must be evaluated, and the order of output elements is not relevant in XBRL, the XBRL semantics would not be impacted.

5 Expression-related Requirements

The requirements here refer to the common features needed in all three of:

· expressions that may be used to bind arguments to facts;

· expressions that may form a Boolean precondition of the formula after arguments are bound; and

· expressions that yield the result of processing a formula (use cases 2, 3 and 4).

Where it is not clear from context elsewhere in the document, these are called binding expressions, precondition expressions, and result expressions, respectively.

5.1 There MUST be only one expression language

From an adoption standpoint, it is not desirable to allow multiple expression languages since that would unnecessarily increase the implementation burden on a compliant formula processor.

Other standards (e.g., XSL and XPointer) have frameworks in which different expressions or scripting languages may be used; new recommendations incrementally extend the set of expressions that must be supported.

Therefore, the requirement that there must be only one expression language MAY be relaxed in a future version of the formula specification.

5.2 The expression language MUST be recognisable to a programmer of average skill.

A “programmer of average skill” means a person familiar with infix and functional notations and able to write spreadsheet formulas, SQL queries, or expressions in a 3GL or 4GL programming language.

This requirement will be satisfied if the expression language is a subset of a widely used language such as ECMAScript or XPATH 1.0. Expression syntaxes ruled out by this requirement include those used by APL, FORTH, LISP, PROLOG, etc.

5.3 The expression language MUST include operators that can select any node in the instance accessible from bound facts.

Fact-binding expressions, conditional expressions and result expressions must be able to operate (for example) on the units of measure, the contexts, and other parts of the input instance. This is believed to be difficult for the formula specification and therefore for an implementation, to prevent this accessibility than it is for an implementation to require it.

5.4 Expressions may include constants.

Expressions must be able to express any constant from the value space of XML Schema primitive data types [SCHEMA‑2].

5.5 Expressions MAY include mathematical operations.

Expressions must be able to express the following operations:

· Addition and subtraction of values;

· Division and modulus of values, both integer and real;

· Multiplication of values;

· Determine maxima and minima of a sequence of values;

· The range of string matching and modification operations made possible by regular expressions;

· All of the following relational operations, =, <, >, <=, >=, and != on numeric items and =, != on non-numeric items.

5.6 Expressions MAY include conditional expressions.

Formulas must be able to express the following operations:

· If, Then, Else

· Elseif

· Switch / Case

Conditional expressions and nested conditionals may test several conditions in sequence.

Example 6: Result expression contains a conditional.

In this example a continuous P/E ratio is mapped to one of three discrete values of Rating.

Formulas:

item	test	result expression	type	matching
Rating		if ($PE lt 5) then 1 else if ($PE gt 10) then 2 else 3	INF

item

test

result expression

type

matching

Rating

if ($PE lt 5) then 1

else if ($PE gt 10) then 2

else 3

INF

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f22	PE	c02	pure	INF	-6.5
f39	Rating	c03	pure	INF	3

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f21	PE	c03	pure	INF	56
f84	Rating	c03	pure	INF	2

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f21	PE	c03	pure	INF	56
f22	PE	c02	pure	INF	-6.5

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f39	Rating	c03	pure	INF	3
f40	Rating	c02	pure	INF	1

In principle, any conditional expression could be recast as a series of separate formulas with disjoint conditions (this example would require three formulas, with one having the condition “5 ≤ PE and PE < 10”).

5.7 Expressions MAY determine the minimum and maximum period that appear among the contexts in an instance.

Expressions may determine the latest and earliest startDate, endDate and instant appearing in the instance. This could also include the use of date expressions that include a function such as now() which would return the current instant as an ISO 8601 string.

Example 7: Formula applies only to the latest period in an instance.

Facts may match the formula only if they fall within a time period that is described as the “latest” period in the instance.

Formulas:

item	test	expression	type	matching
AssetEquity	($Equity gt 0)	$Assets div $Equity	precision=18	p-equal, u-equal, c-equal; Context must have a period that is the latest occurring in the input instance.

item

test

expression

type

matching

AssetEquity

($Equity gt 0)

$Assets div $Equity

precision=18

p-equal, u-equal, c-equal;

Context must have a period that is the latest occurring in the input instance.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f01	Assets	c02	usd	INF	100000
f03	Equity	c02	usd	INF	17000
f86	AssetEquity	c02	usd	9	58.82352941
f13	Assets	c03	usd	INF	43000
f15	Equity	c03	usd	INF	26000
f31	AssetEquity	c03	pure	18	1.653846153846153846

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f13	Assets	c03	usd	INF	43000
f15	Equity	c03	usd	INF	26000
f87	AssetEquity	c03	pure	9	58.83252941

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f01	Assets	c02	usd	INF	100000
f03	Equity	c02	usd	INF	17000
f13	Assets	c03	usd	INF	43000
f15	Equity	c03	usd	INF	26000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f31	AssetEquity	c03	pure	18	1.653846153846153846

In this example, one pair of facts (f01 and f03) evaluates the condition to false and the other (f13 and f15) evaluates it to true. The latest period among the inputs is the instance 2003‑12‑31.

This applies to use cases 1, 2, 3, and 4.

5.8 Expressions may test for the presence of a fact for any concept in any context.

The presence or absence of a fact may be tested.

See Example 6 for an example in a conditional expression, Example 24 for an example in binding expressions; Example 23 also indicates that Nil items may be tested for.

This applies to use cases 1, 2, 3, and 4.

5.9 All facts must be bound before an expression is evaluated.

Although in principle, expressions such as or(x,y,z) could be evaluated left-to-right and with x="true", neither y nor z would need to be bound, formula processing does not support this.

Example 8: Expression evaluation requires all facts to be bound.

Formulas:

item	test	expression	type	matching
AssetsOkay		$AssetsUB and $AssetsLB	Boolean	p-equal, c-equal.

Facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f49	AssetsUB	c03			false

Result:

@id	item	@contextRef	@unitRef	@precision	[content]

In this example, even though AssetsLB is not strictly needed to evaluate the expression, the output still should not contain the result that AssetsOkay is false

5.10 The behaviour of a formula processor MUST be defined in the case of an expression evaluation exception.

A formula will bind arguments to facts, and substitution of the arguments as variables in the expression allows the expression to be evaluated. The formula specification must indicate, in particular, what result if any is produced when the expression throws an exception when evaluated.

A try/catch mechanism would allow the formula author to control the behaviour on a case-by-case basis. This presumably though not always will include the generation of a human-readable error message.

This applies to use cases 1, 2, 3, and 4.

5.11 Constants MAY be named and defined inside a formula and referenced in its expressions.

Formulas often refer to constants that may appear locally.

Example 9: Formula uses a locally defined symbolic constant.

In this formula, lowerTolerance and upperTolerance are constants bound to “-500” and “500” respectively.

Formulas:

item	test	expression	type	matching
AssetsOkay		($lowerTolerance lt ($Assets - ($CurrentAssets + $FixedAssets)) and (($Assets – ($CurrentAssets + $FixedAssets) lt $upperTolerance)		p-equal, u-equal and c-equal;

item

test

expression

type

matching

AssetsOkay

($lowerTolerance lt

($Assets - ($CurrentAssets + $FixedAssets))

and

(($Assets – ($CurrentAssets + $FixedAssets)

lt $upperTolerance)

p-equal,

u-equal and

c-equal;

Use cases 1 and 2 (AssetsOkay is not an explicit concept):

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f48	Assets	c03	usd	INF	43400

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Use cases 3 and 4 (AssetsOkay is an explicit concept):

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Result facts:

@id	item	@contextRef			[content]
f48	AssetsOkay	c03			false

5.12 Constants may be named and defined outside a formula and referenced in its expressions.

Sets of formulas often refer to constants that appear in several related formulas; there must be a way to define a constant whose scope is an entire set of formulas. There must be a means to limit the scope of such a constant, such as by using the xlink:role attribute.

Example 10: Formula uses a globally defined symbolic constant.

Here, tolerance is bound to “500” globally and so has the identical value in two different formulas, one for testing the upper bound (UB) and one for the lower bound (LB).

Formulas:

item	test	expression	type	matching
AssetsUB		($Assets - ($CurrentAssets + $FixedAssets)) lt $tolerance	Boolean	p-equal, u-equal and c-equal;
AssetsLB		$tolerance lt ($Assets - ($CurrentAssets + $FixedAssets))	Boolean	p-equal, u-equal and c-equal;

item

test

expression

type

matching

AssetsUB

($Assets - ($CurrentAssets + $FixedAssets))

lt $tolerance

Boolean

p-equal,

u-equal and

c-equal;

AssetsLB

$tolerance lt

($Assets - ($CurrentAssets + $FixedAssets))

Boolean

p-equal,

u-equal and

c-equal;

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000
f49	AssetsUB	c03			false
f50	AssetsLB	c03			true

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000
f89	AssetsUB	c03			true

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Result facts:

@id	item	@contextRef	[content]
f49	AssetsUB	c03	false
f50	AssetsLB	c03	true

5.13 Functions MAY be named and expressions defined outside a formula and referenced in its expressions

Any function that is not “built in” to the expression language – for example, trigonometric functions – would either have to be defined repeatedly in every formula that needed it, or an intermediate item defined in the taxonomy whose only role would be to hold the result of the formula and then append that result to an instance so that its value could be bound in all formulas that may need it. Examination of UK Inland Revenue Tax Computation use cases, similar items on the FFIEC 031 and 041 forms, and consideration of many financial analysis routines, reveals that the same formulas are used again and again.

Example 11: Formula uses a globally defined function.

In this formula, there is a reference to an externally defined function:

declare function my:withinTolerance( $x as xdt:anyAtomicType, $y as xdt:anyAtomicType ) as xdt:boolean* { fn:abs( $x - $y) lt 500 }

Formulas:

item	test	expression	type	matching
AssetsOkay		my:withinTolerance ($Assets,($CurrentAssets + $FixedAssets))	Boolean	p-equal, u-equal and c-equal;

item

test

expression

type

matching

AssetsOkay

my:withinTolerance

($Assets,($CurrentAssets + $FixedAssets))

Boolean

p-equal,

u-equal and

c-equal;

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Result facts:

@id	item	@contextRef			[content]
f48	AssetsOkay	c03			false

5.14 Functions MAY have their scope defined to apply to only a subset of formulas in a set

There must be a way to limit the scope of such a function definition to be usable only within a certain set of formulas, such as by using the xlink:role attribute.

Example 12: Different formulas bind the same name to different functions.

In two different formulas, there are references to externally defined functions that apply in different rules within the same set. The rules are not distinguished by an arithmetic test but rather by an indicator such as xlink:role.

scope

function

Taxation Enforcement

declare function tax:withinTolerance( $x as xdt:anyAtomicType, $y as xdt:anyAtomicType ) as xdt:boolean* { fn:abs( $x - $y) lt 500 }

Securities Enforcement

declare function sec:withinTolerance( $x as xdt:anyAtomicType, $y as xdt:anyAtomicType ) as xdt:boolean* { fn:abs( $x - $y) lt 5000000 }

Formulas:

item

test

expression

type

matching

AssetsOkay

$Enforcement eq “Securities Enforcement”

tax:withinTolerance ($Assets,($CurrentAssets + $FixedAssets))

Boolean

p-equal,

u-equal and

c-equal;

EarningsOkay

$Enforcement eq “Taxation Enforcement”

sec:withinTolerance ($Equity,$EquityPrev + $Earnings)

Boolean

p-equal, u-equal;

“EquityPrev” refers to a context in the year previous to that of “Equity”.

The duration-type period of “Earnings” must begin at the instant represented by “EquityPrev”.

Both computations have 1000-dollar errors but only one of them results in a false value.

Use cases 1 and 2 (AssetsOkay and EarningsOkay are not explicit concepts):

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f03	Equity	c02	usd	INF	17000
f09	Earnings	c01	usd	INF	9000
f11	Equity	c03	usd	INF	27000

Use cases 3 and 4 (AssetsOkay and EarningsOkay are explicit concepts):

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000
f03	Equity	c02	usd	INF	17000
f09	Earnings	c01	usd	INF	9000
f11	Equity	c03	usd	INF	27000

Result facts:

@id	item	@contextRef	[content]
f48	AssetsOkay	c03	True
f74	EarningsOkay	c03	False

5.15 Expression evaluation exceptions MAY be caught to produce a result

The expression language must support a try/catch or other exception handling mechanism and allow the expression to produce a result. The following is only an example result and is not meant to be normative for all formulas.

Example 13: Catching an exception

Formulas:

item

test

expression

matching

EPS

Try ($Earnings div $AvgShares)

Catch Exception

Return <EPS>0</EPS>

p-equal, c-equal.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f72	AvgShares	c01	shs	INF	0
f90	EPS	c01	usdsh	INF	0

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f72	AvgShares	c01	shs	INF	0
f37	EPS	c01	usdsh	c01	0.16363636

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f72	AvgShares	c01	shs	INF	0

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f90	EPS	c01	usdsh	INF	0

Note that the units, context and precision of the result remain the same as if the calculation had not thrown an exception; only its content is different.

6 Fact-binding Requirements

The requirements here refer to the features needed to bind facts to the arguments for the formula as they appear in the condition and result expressions.

6.1 Formulas MAY filter the input facts to which they apply according to relationships between facts in one or more contexts.

The facts bound in a formula may have different contexts.

Contexts are related to one another using the following orderings:

· The relationship “after” that partially orders periods;

· The subset relationship “during” between periods;

· The subset relationship implied between an entity and its segments {4.7.3};

· The subset relationship implied between an empty (universal) scenario and a scenario with additional discriminators {4.7.4}.

Example 14: Formula binds items that are p-equal and u-equal in identical contexts

An important type of formula involves a mathematical operator applied to a pair of items when they are p-equal, c-equal and u-equal.

Formulas:

item	test	expression	type[1]	matching
Assets		$CurrentAssets + $FixedAssets	INF	p-equal, c-equal and u-equal

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f34	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	43000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f34	FixedAssets	c03	usd	INF	35000
f48	Assets	c03	usd	INF	43400

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f34	FixedAssets	c03	usd	INF	35000

Result facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f13	Assets	c03	usd	INF	43000

Example 15: Formula binds items that are p-equal, u-equal and c-equal

A variation of Example 14 is when items are c-equal without the contexts being identical.

Formulas:

item	test	expression	type	matching
Assets		$CurrentAssets + $FixedAssets	INF	p-equal, c-equal and u-equal

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c06	usd	INF	35000
f13	Assets	c03	usd	INF	43000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c06	usd	INF	35000
f48	Assets	c03	usd	INF	43400

Use cases 3 and 4:

Facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c06	usd	INF	35000

Result:

@id	item	@contextRef	@unitRef	Precision	[content]
f13	Assets	c03	usd	INF	43000

The output context is s-equal to c03 and c06. Formula processors should behave consistently and the specification must define which context to use on output.

Example 16: Formula binds items that are p-equal, u-equal and contexts whose periods differ

Formulas must be able to express relations that cross periods. In this example the value of any two values for “Shares” that differ by one year are averaged during the intervening duration.

Formulas:

item

test

expression

type

matching

AvgShares

($SharesNext + $Shares) div 2

INF

p-equal, u-equal;

“SharesNext” is in a context offset by one year from “Shares”.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f05	Shares	c02	shs	INF	50000
f17	Shares	c03	shs	INF	60000
f11	AvgShares	c01	shs	INF	55000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f05	Shares	c02	shs	INF	50000
f17	Shares	c03	shs	INF	60000
f12	AvgShares	c01	shs	INF	5000

Use cases 3 and 4:

Facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f05	Shares	c02	shs	INF	50000
f17	Shares	c03	shs	INF	60000

The output context, because it is not present among the input facts, must be synthesised by the formula. In this example it happens to be s-equal to c01. Note that the two inputs are in “instant” contexts while the output is a “duration” context whose start and end dates are equal to those of the input instants (taking into account differences in the way startDate and endDate default the time of day {4.7.2}).

Result:

@id	item	@contextRef	@unitRef	Precision	[content]
f11	AvgShares	s-equal to c01	shs	INF	55000

The matching of input periods may involve matching of endpoints. More generally, endpoints may match in any relationship expressible by using comparison operators (equal, less than, greater than), arithmetic offsets (plus, minus), and constants (dates, datetimes, durations).

Example 17: Formula binds items in contexts that match period endpoints

This example is a simple movement analysis on the value of Equity.

Formulas:

item

test

expression

type

matching

Equity

$EquityPrev + $Earnings

INF

p-equal, u-equal;

“EquityPrev” refers to a context in the year previous to that of “Equity”.

The duration-type period of “Earnings” must begin at the instant represented by “EquityPrev”.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f03	Equity	c02	usd	INF	17000
f09	Earnings	c01	usd	INF	9000
f11	Equity	c03	usd	INF	26000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f03	Equity	c02	usd	INF	17000
f09	Earnings	c01	usd	INF	9000
f94	Equity	c03	usd	INF	0

Use cases 3 and 4:

Facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f03	Equity	c02	usd	INF	17000
f09	Earnings	c01	usd	INF	9000

Result:

@id	item	@contextRef	@unitRef	Precision	[content]
f11	Equity	s-equal to c03	usd	INF	26000

6.2 Formulas MAY restrict the facts that they bind based on their context

This requirement also implies that the expression language SHOULD provide a native library of date manipulation functions such as those specified for XQuery and XPath [XQPFO].

Example 18: Formula binds facts in different segments

A fixed asset breakdown between an entity (444) and its segments (aaa and bbb) has the formula shown below, and the two figures 50,000 and 80,000 summing to 130,000.

The presumption of this use case is that if there is no segment element, this corresponds to the “universal” segment, i.e., the entire entity.

Formulas:

item

test

expression

type

matching

FixedAssets

$FixedAssetsaaa + $FixedAssetsbbb

INF

p-equal, u-equal;

FixedAssets(aaa) and FixedAssets(bbb) contexts are s‑equal except for the segment identifier (aaa and bbb, respectively).

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f41	FixedAssets	c08	usd	INF	50000
f42	FixedAssets	c10	usd	INF	80000
f43	FixedAssets	c05	usd	INF	130000

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f41	FixedAssets	c08	usd	INF	50000
f42	FixedAssets	c10	usd	INF	80000
f92	FixedAssets	c05	usd	INF	260000

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f41	FixedAssets	c08	usd	INF	50000
f42	FixedAssets	c10	usd	INF	80000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f43	FixedAssets	c05	usd	INF	130000

Note that the XML elements aaa and bbb, which are to be used in the input instance, must be present in a namespace accessible to the formulas, just like the item names and other parts of a taxonomy.

Example 19: Formula binds facts in different scenarios

The Earnings of an entity are reported as actual and budgeted in different scenarios, and in yet a third scenario the variance figure is to be computed from them.

There is no presumption in this use case is that if there is no scenario element that it means some kind of “universal” scenario; rather, scenario is simply unspecified.

Note that the XML elements actual, budgeted and variance, which are to be used in the input instance, must be present in a namespace accessible to the formulas, just like the item names and other parts of a taxonomy.

Formulas:

item

test

expression

type

matching

Earnings(variance)

$EarningsActual – $EarningsBudgeted

INF

p-equal, u-equal;

Earnings(actual), Earnings(variance) and Earnings(budgeted) contexts are s‑equal except for the scenario identifier.

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f44	Earnings	c11	usd	INF	12000
f45	Earnings	c12	usd	INF	14000
f46	Earnings	c13	usd	INF	-2000

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f44	Earnings	c11	usd	INF	12000
f45	Earnings	c12	usd	INF	14000
f93	Earnings	c13	usd	INF	-30000

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f44	Earnings	c11	usd	INF	12000
f45	Earnings	c12	usd	INF	14000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f46	Earnings	c13	usd	INF	-2000

Example 20. Formula binds facts across segments of a common entity

Two fixed asset breakdowns between:

· an entity (444);

· its geographic segments (<geo>ON</geo> and <geo>MI</geo>); and

· line of business segments (<lob>paper</lob> and <lob>plastic</lob>)

have the formula shown below, with the two sets of figures 50,000 and 80,000 and 40,000 and 90,000 separately summing to 130,000.

Formulas:

item

condition

expression

type

matching

FixedAssets

sum of FixedAssets*

INF

p-equal, u-equal;

FixedAssets* contexts have a common entity, common segment element and distinct segment element contents,

FixedAssets* contexts have s‑equal scenarios;

Result context entity has no segment element.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f41	FixedAssets	c08	usd	INF	50000
f42	FixedAssets	c10	usd	INF	80000
f75	FixedAssets	c18	usd	INF	40000
f76	FixedAssets	c19	usd	INF	90000
f43	FixedAssets	c05	usd	INF	130000

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f41	FixedAssets	c08	usd	INF	50000
f42	FixedAssets	c10	usd	INF	80000
f75	FixedAssets	c18	usd	INF	40000
f76	FixedAssets	c19	usd	INF	90000
f92	FixedAssets	c05	usd	INF	260000

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f41	FixedAssets	c08	usd	INF	50000
f42	FixedAssets	c10	usd	INF	80000
f75	FixedAssets	c18	usd	INF	40000
f76	FixedAssets	c19	usd	INF	90000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f43	FixedAssets	c05	usd	INF	130000
f77	FixedAssets	c05	usd	INF	130000

By contrast with the previous example, in this example the formula is not limited to known segment names. Rather, the formula match criteria MUST be written in conjunction with a design of segment child elements that ensures distinct child elements of segment are treated as orthogonal and distinct element contents are comprehensive and non‑overlapping

6.3 Formulas MAY restrict the facts that they bind based on their unit.

See Example 31.

6.4 Formulas MAY restrict the facts that they bind based on their precision or decimals attribute.

The condition on the facts may allow precision, decimals, or both, and comparative operators on their values.

6.5 Formulas MAY filter input facts depending on their surrounding tuple structure

Formulas MUST be able to use predicates that use paths with the parent-child and other XPATH axes in order to filter input facts. These paths MAY refer to facts already bound.

6.6 Formulas MAY filter input facts based on the filters applied in that formula to other facts

For example, an input may be filtered according to a criterion such as “the same context as that other argument, except one quarter earlier.”

6.7 Formulas MUST only bind facts that are explicitly present in the input

There is no requirement that formulas automatically match to facts derived from previous formulas matched and evaluated.

This requirement does not apply in use cases 1 and 2.

Example 21. Formula produces a default fact in the absence of a matching fact

When Current Assets are known in a given context but Fixed Assets are not, a formula author may want to assert a default value (zero) for the item FixedAssets.

The conditions expressed in this formula would be evaluated sequentially in the sense that the formula only applies in a context where CurrentAssets is already bound. The function fn:not is used as the predicate "unbound”, in effect assuming that “unbound” variables are initially bound to the empty sequence until bound to something else by the formula processor".

Note also that fact f43 will appear in the output, not the input, so that any formulas that required input facts for CurrentAssets and FixedAssets in c-equal contexts would require additional formula processor iterations.

Formulas:

item

test

expression

type

matching

FixedAssets

$CurrentAssets

and

fn:not($FixedAssets)

INF

p-equal, u-equal and c-equal;

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f33	CurrentAssets	c03	usd	INF	8000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f43	FixedAssets	c03	usd	INF	0

Example 22: Formula assumes default values in the absence of matching facts

When values are not known in a given context, a formula author may assume a default value (zero) for items, in this example, default values of zero for CurrentAssets and FixedAssets.

Formulas:

item

test

expression

type

matching

Assets

$CurrentAssets + $FixedAssets

INF

p-equal, c-equal and u-equal;

If CurrentAssets unbound then CurrentAssets = 0;

If FixedAssets unbound then FixedAssets = 0;

If both are unbound the formula produces no result.

Use cases 1 and 2:

This set of facts covers each of the three possible binding cases in the formula.

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f77	CurrentAssets	c02	gbp	INF	2000
f65	FixedAssets	c16	gbp	INF	5000
f13	Assets	c03	usd	INF	43000
f64	Assets	c02	gbp	INF	2000
f66	Assets	c16	gbp	INF	5000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f77	CurrentAssets	c02	gbp	INF	2000
f65	FixedAssets	c16	gbp	INF	5000
f48	Assets	c03	usd	INF	43400
f02	Assets	c02	gbp	INF	43000
f91	Assets	c16	gbp	INF	10000

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f77	CurrentAssets	c02	gbp	INF	2000
f65	FixedAssets	c16	gbp	INF	5000

Result facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f13	Assets	c03	usd	INF	43000
f64	Assets	c02	gbp	INF	2000
f66	Assets	c16	gbp	INF	5000

Example 23: Formulas ignore Nil facts by default but may bind them

Formula authors must have the choice whether or not to bind expressions with nil facts. At least for the purpose of describing formulas in these examples the assumption is that the default is that nil facts are not bound, and so nothing appears in the “test” column.

The Assets rule should produce no results. Furthermore, if the formula had instead assigned a default value of zero to CurrentAssets then it should behave the same as Example 22 above. This suggests that this example represents a somewhat more robust treatment than use case Error! Reference source not found., which would involve creating a new fact that would then be a duplicate {4.10} of the nil item.

The Rating formula should produce one item as a result.

Formulas:

item

test

expression

type

matching

Assets

$CurrentAssets + $FixedAssets

INF

p-equal, c-equal and u-equal.

Rating

element(my:PE, xbrli:decimalItemType nillable)

if ( $PE[@xsi:nil = “true”]) then 0

else if ($PE lt 5) then 1

else if ($PE lt 10) then 2

else 3

INF

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f68	CurrentAssets	c03	usd	INF	(xsi:nil)
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	43000

Inconsistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f70	PE	c02	pure	INF	(xsi:nil)
f40	Rating	c02	pure	INF	1

Use cases 3 and 4:

Facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f68	CurrentAssets	c03	usd	INF	(xsi:nil)
f35	FixedAssets	c03	usd	INF	35000
f70	PE	c02	pure	INF	(xsi:nil)

Result:

@id	item	@contextRef	@unitRef	Precision	[content]
f71	Rating	c02	pure	INF	0

6.8 Formulas MAY specify preconditions on expressions based on context and fact value

For example, an expression may apply only when the value of a certain item is nonzero in the bound context. The requirement is that there be a way to “abort” the application of a formula after all inputs are bound to facts, but before its expression is evaluated.

This does not require that the matching and binding criteria of any argument be able to reference the value of any other bound argument. For example, a formula that binds argument “S” to the “SignatureDate” of a financial statement does not need to be able to use the date “S” to find the Revenue value as of date “S”. In general, computed offsets (e.g., the binding of one argument determines which of many different time periods the other arguments are bound in) do not have to be supported.

Setting a precondition on an item value may be needed to ensure the expression is meaningful and will not cause an evaluation error.

Example 24: Formula has a precondition on item values

This is an example in which the condition of one pair of facts (f19 and f29) evaluates to true, the other pair (f20 and f30) to false.

Formulas:

item

test

expression

type

matching

($EPS gt 0)

($Price div $EPS)

INF

p-equal, u-equal;

Context of “Price” has a period that is the instant which ends that of “EPS”.

Use cases 1 and 2:

(PE would normally have a data type of non-negative decimal, making these particular examples somewhat artificial):

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f20	Price	c03	gbpsh	INF	5.2
f30	EPS	c01	gbpsh	INF	-0.8
f22	PE	c03	pure	INF	-56

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f19	Price	c03	usdsh	INF	11.2
f29	EPS	c01	usdsh	INF	.2
f23	PE	c03	pure	INF	-56

Use cases 3 and 4:

Facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f19	Price	c03	usdsh	INF	11.2
f29	EPS	c01	usdsh	INF	.2
f20	Price	c03	gbpsh	INF	5.2
f30	EPS	c01	gbpsh	INF	-0.8

Result:

@id	item	@contextRef	@unitRef	@precision	[content]
f21	PE	c03	pure	INF	56

Example 25: Formula applies only to certain time periods

Facts may match the formula only if they fall within a named time period. Note that because every item has a fixed periodType, it is not necessary to be able to specify the kind of period of which the fact is asserted, because that is implicit in the item itself.

In this example, one pair of facts (f01 and f03) evaluates the condition to true and the other (f13 and f15) evaluates it to false.

Formulas:

item

test

expression

type

matching

AssetEquity

($Equity gt 0)

$Assets div $Equity

precision=10

p-equal, u-equal, c-equal;

Context must have a period

whose endpoint is strictly

before 2003‑01‑01.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f13	Assets	c03	usd	INF	43000
f15	Equity	c03	usd	INF	26000
f87	AssetEquity	c03	pure	10	58.82352941

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f01	Assets	c02	usd	INF	100000
f03	Equity	c02	usd	INF	17000
f86	AssetEquity	c02	pure	10	58.82352941

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f01	Assets	c02	usd	INF	100000
f03	Equity	c02	usd	INF	17000
f13	Assets	c03	usd	INF	43000
f15	Equity	c03	usd	INF	26000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f31	AssetEquity	c02	pure	10	5.882352941

Example 26: Precondition tests date items in historical period

Setting a precondition on an item value may be part of defining its scope of applicability.

In this example, historical data (Acquisition Cost, Useful Life, and Acquisition Date) of an asset determines its write down allowance for all future periods. Acquisitions made after 11 March 1992 are subject to a GBP 2000 maximum write-down per year; hence the acquisition date of 10 October 1993 means that after two years only GBP 4000 has been written down, not 2*(20000/6) had the acquisition been made (say) 1991.

In this example the context of the Write-Down Allowance is determined from the context of a nonzero Write-Down Value Brought Forward. The item UsefulLife is a durationItemType but the result of the expression is cast to the same type and unit as AcquisitionCost.

Formulas:

item

test

expression

type

matching

WriteDownAllowance

($AcquisitionDate lt 1992-03-11) and

($WDVBroughtForward gt 0)

$AcquisitionCost div fn:get-years-from-yearMonthDuration‌($UsefulLife)

INF

p-equal, c-equal;

Result context is that of a nonzero WDVBroughtForward whose period is greater than or equal to the input facts’ end date.

WriteDownAllowance

($AcquisitionDate ge 1992-03-11) and

($WDVBroughtForward gt 0)

fn:min(2000, $AcquisitionCost div fn:get-years-from-yearMonthDuration‌($UsefulLife))

INF

p-equal, c-equal;

Result context is that of a nonzero WDVBroughtForward whose period is greater than or equal to the input facts’ end date.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f57	AutoWriteDown				(tuple)
f58	AssetName	c14			571XVH
f59	AcquisitionDate	c14			1993-10-10
f60	AcquisitionCost	c14	gbp	INF	20000
f61	UsefulLife	c14			6
f62	WDVBroughtForward	c15	gbp	INF	16000
f63	WriteDownAllowance	c15	gbp	INF	2000

Inconsistent facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f57	AutoWriteDown				(tuple)
f58	AssetName	c14			571XVH
f59	AcquisitionDate	c14			1993-10-10
f60	AcquisitionCost	c14	gbp	INF	20000
f61	UsefulLife	c14			6
f62	WDVBroughtForward	c15	gbp	INF	16000
f80	WriteDownAllowance	c15	gbp	INF	2400

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f57	AutoWriteDown				(tuple)
f58	AssetName	c14			571XVH
f59	AcquisitionDate	c14			1993-10-10
f60	AcquisitionCost	c14	gbp	INF	20000
f61	UsefulLife	c14			6Y
f62	WDVBroughtForward	c15	gbp	INF	16000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f63	WriteDownAllowance	c15	gbp	INF	2000

Figure 5: Formula applies only to certain units

Facts may bind in the formula only if the units match.

Formulas:

item

test

expression

type

matching

AssetEquity

($Equity gt 0)

$Assets div $Equity

precision=10

p-equal, u-equal, c-equal;

Assets context must have unit/measure = ISO4217:USD

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f01	Assets	c02	usd	INF	100000
f03	Equity	c02	usd	INF	17000
f02	Assets	c02	gbp	INF	43000
f04	Equity	c02	gbp	INF	26000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f31	AssetEquity	c02	pure	10	5.882352941

In this example, one pair of facts (f01 and f03) evaluates the condition to true and the other (f02 and f04) evaluates it to false.

6.9 Formulas MAY bind facts that are present in more than one XBRL instance within a single root XML element

The motivation for this is that some formulas will require multiple XBRL instances, if only because a given instance may require more than one formula processing iteration. Because all identifiers—particularly the id attributes of unit and context elements—cannot be duplicated in an XML element, simple concatenation within a parent element may not be significantly easier than actually merging the two instances properly to create a single XBRL-valid instance. Nevertheless the requirement remains.

6.10 Multiple applications of a formula to a set of facts, with multiple combinations of bindings of arguments to facts, may produce multiple results

A formula may match the same facts to different arguments and apply multiple times.

6.11 Formula bindings and behaviour MUST be defined in situations in which duplicates appear in the input instance

When duplicate facts appear in an instance, a single formula could:

(a) repeatedly bind different duplicate facts and re-evaluate its expression repeatedly,

(b) follow the approach used in the calculation linkbase and derive no facts, or

The specification MUST indicate what facts if any are bound in this situation. The specification MUST use an approach consistent with interpretation of XBRL 2.1 {5.2.5.2}.

Example 27: Formula does not bind duplicate facts.

In XBRL 2.1 {5.2.5.2} duplicate facts do not bind in summation-item calculations (“A calculation binds for a summation item if it has no duplicates in the XBRL instance...”) or if the facts have nil values (“Items with nil values do not participate in calculation bindings”). The same approach applies consistently in formulas.

This formula produces no results because f33 and f69 satisfy the XBRL 2.1 “duplicates” predicate. Furthermore, this case is distinct from the absence of CurrentAssets and therefore a formula specifying a default value should not appl

Formulas:

item	test	expression	type	matching
Assets		$CurrentAssets + $FixedAssets	INF	p-equal, c-equal and u-equal.

Use cases 1 and 2:

Consistent facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f69	CurrentAssets	c03	usd	INF	10000
f35	FixedAssets	c03	usd	INF	35000
f48	Assets	c03	usd	INF	43400

Use cases 3 and 4:

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f69	CurrentAssets	c03	usd	INF	10000
f35	FixedAssets	c03	usd	INF	35000

Result facts:

@id

item

@contextRef

@unitRef

Precision

[content]

6.12 Formula arguments MUST bind to facts, not to their contents

This requirement is a logical consequence of other requirements such as 6.5 above, “Formulas MAY filter input facts depending on their surrounding tuple structure”

6.13 Constants MAY be facts

This requirement is a logical consequence of 6.12 above. Requirement 5.4 above, “Expressions may include constants.”, presumes that constants consist only of numbers, strings and other primitive data types, however, if formula arguments are bound to facts then constants must also be able to represent facts having a precision, context, and units.

6.14 A variable number of facts may be bound

Arguments bound in a formula may be bound to a sequence of facts for execution. Formulas such as “the sum of all revenues for years before 2001” and “the sum of values of the children of the item” are allowed. This will require operations on vectors and matrices spanning any number of contexts, which in turn requires a definition of the “best” or “maximal” match in order to avoid a combinatorial explosion. For example, if argument X is defined in six periods, then the “moving average of X” must be defined with respect to a fixed number of periods anyway (2 periods? 3 periods?), and this can adequately be expressed using formulas with a fixed number of input arguments. By contrast, if X is “the sum of X for all child entities,” all could mean “all child entities for which X is known in each known period” or “all child entities for which X is known in all periods.”

7 Signalling Requirements

Instead of producing only a Boolean result as in use cases 3 or 4, or simply signalling an overall failure as in use case 1, in use case 3 a formula can produce a more detailed warning or explanation of a problem.

Example 28: Formula produces a diagnostic message.

Formulas:

item

test

expression

type

matching

AssetsMessage

fn:not ($lowerTolerance lt

($Assets - ($CurrentAssets + $FixedAssets))

and

(($Assets – ($CurrentAssets + $FixedAssets)

lt $upperTolerance)

fn:concat("Assets of ",$Assets," are outside the range (",$lowerTolerance,", ",$upperTolerance,") compared to ",$CurrentAssets," + ",$FixedAssets")

p-equal,

u-equal and

c-equal;

Input facts:

@id	item	@contextRef	@unitRef	Precision	[content]
f33	CurrentAssets	c03	usd	INF	8000
f35	FixedAssets	c03	usd	INF	35000
f13	Assets	c03	usd	INF	44000

Results:

The formula produces the warning (use case 2):

Assets of 44000 are outside the range (-500,500) compared to 35000 + 44000

Or a message item (use case 3):

@id

item

@contextRef

[content]

f48

AssetsMessage

c03

"Assets of 44000 are outside the range (-500,500)

compared to 35000 + 44000”

8 Result Expression Requirements

Unless otherwise noted, the “expressions” referred to here refer to all three of:

· expressions that are used to bind arguments;

· expressions that form the Boolean precondition of the formula; and

· the expression that yields the result of the formula.

These requirements apply only to use cases 3 and 4; however, specifications covering use case 2 may require similar expressions so as to produce user-specified consistency signals.

8.1 If the application of a formula results in an item then the formula must fully determine the context of that item

The context is determined on the basis of the formula itself, the information in the contexts of the facts being drawn upon by the formula, and the facts bound to variables in the expression when the formula matches.

8.2 If the application of a formula results in a numeric item, then the formula processor must also result in a unit reference and a precision or decimals attribute

The unit reference and the precision and decimals attributes are determined on the basis of the formula itself and the information in the facts bound to variables in the expression when it applies {4.6}. Furthermore, the formula author must be able to specify the unit, precision, and decimals attributes in addition to the requirement is that the formula processor be able to determine them on its own. If the result item is a numeric type then the formula must specify the result units; there is no default.

Example 29: Expression yields a new unit of measure.

The units of measure of inputs, when multiplied or divided, may yield a different unit of measure. The unit of measure need not have been previously defined in the input instance. In this example there are no facts with the unit representing “USD per share”; it is synthesised by the formula for the output. In this example the precision of the output is infinite, just like the inputs.

Formulas:

item	test	expression	matching
EPS		($Earnings div $AvgShares)	p-equal, c-equal.

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f36	Earnings	c01	usd	INF	11000
f11	AvgShares	c01	shs	INF	55000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f29	EPS	c01	usdsh	INF	0.2

Example 30: Formula determines the result units of an expression from the units of the bound facts.

The units of measure of outputs differ depending on the units of the input facts that were bound. If the result item is a numeric type then the formula specifies the result units as a function of the input units.

In this example the same formula computes results in the same context having different units depending on which of two input facts (f09 and f10) were used in the computation. The item specified in the result (e.g., EPS) determines the item type (e.g., pureItemType) and therefore constrains the possible units (e.g. pure) {4.8.2}.

Rejected requirement 11.5 below, “* Formulas MAY specify one or more alternative items or tuples as the possible result of expression evaluation,” would allow a formula to produce either a decimal or a fraction as the result of a division, but without it the result will always be one or the other.

Formulas:

item

test

expression

type

matching

EPS

($Earnings div $AvgShares)

precision=9 and

units(result) = units(Earnings) / units(AvgShares)

p-equal, c-equal.

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f09	Earnings	c01	usd	INF	9000
f10	Earnings	c01	gbp	INF	5000
f11	AvgShares	c01	shs	INF	55000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f37	EPS	c01	usdsh	9	0.16363636
f38	EPS	c01	gbpsh	9	0.09090909

Example 31: Formula overrides the natural result units of an expression.

In this example the units of the Write-Down Allowance that would be determined from the inputs would be a currency amount “per year”, but the formula must type cast the output to the currency that matches the currency of WriteDownAllowance which is a monetaryItemType and therefore must have a unit whose measure is an ISO currency type {4.8.2}. The example shows that the currency (or any other part of the unit) cannot be “hard wired” into the formula but MUST be determined from the input facts.

Formulas:

item

test

expression

type

matching

WriteDownAllowance

$AcquisitionCost div fn:get-years-from-yearMonthDuration‌($UsefulLife)

precision=INF and

units(result) = units(AcquisitionCost)

p-equal, c-equal;

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f76	UsefulLife	c15			5Y
f78	AcquisitionCost	c15	gbp	INF	12000
f79	AcquisitionCost	c15	usd	INF	20000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f80	WriteDownAllowance	c15	gbp	INF	2400
f81	WriteDownAllowance	c15	usd	INF	4000

Example 32: Expression result has limited precision.

When an expression containing the division operator uses a fact with precision="INF" as a divisor, and the result fact of the expression has a denominator with prime factors other than 2 and 5 the result is a repeating decimal without a finite representation.

The precision of a repeating decimal when not otherwise specified will be INF even though its lexical representation is limited to the number of digits of precision available on the executing hardware. This reflects the underlying reality of limited machine precision. Formula authors may choose to limit the precision still further. Moreover, if different processors were allowed to select their own output precision, formulas would yield different results on different machines. Therefore, formulas must be able to specify the desired precision of the output.

The quotient 9000/55000 yields a repeating decimal (.1636363…) whose lexical representation is limited to 18 digits by the default data type (double) of the executing processor.

Formulas:

item

test

expression

type

matching

EPS

($Earnings div $AvgShares)

precision=8

p-equal, u-equal, c-equal.

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f09	Earnings	c01	usd	INF	9000
f11	AvgShares	c01	shs	INF	55000

Result facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f37	EPS	c01	usdsh	8	0.1636363636363636363

Example 33: Expression result has limited number of decimal places.

The result may also be specified to a number of decimal places rather than by precision.

Formulas:

item	test	expression	type	matching
EPS		($Earnings div $AvgShares)	decimals=7	p-equal, u-equal, c-equal.

Input facts:

@id	item	@contextRef	@unitRef	@precision	[content]
f09	Earnings	c01	usd	INF	9000
f11	AvgShares	c01	shs	INF	55000

Result facts:

@id	item	@contextRef	@unitRef	@decimals	[content]
f38	EPS	c01	usdsh	7	0.1636364

8.3 Formulas MAY include expressions to construct a derived item

Each formula MAY specify how new elements are to be constructed as a consequence of the presence and content of other facts in an instance. All parts of the result item MUST be specifiable by the formula, including element names, content of each element, context, and in the case of numeric facts, the unit and either decimals or precision attributes.

8.4 Formulas MAY include expressions to construct a derived context

8.5 Formulas MAY include expressions to construct a derived unit

8.6 Formulas MAY create the content of a new item

For example, a formula that derives the “cash” at end of period as [“cash” (at the beginning of period) + collections – disbursements”] may calculate the value as of the end of 2003 from the value at the beginning of 2003 and values during the period 2003-01-01 to 2003-12-31, which are two distinct contexts also distinct from the context of the ending value.

The result of a single application of a formula to a set of facts may be a single fact.

8.7 A formula MUST be able to create contexts, units, and items that were not present in the input document

Output instances may contain elements from any taxonomy namespace present in the input document, and may produce new context and unit elements.

Formulas do not have to provide a way to synthesize namespaces, elements or attributes that are not already present in the instance being processed, the DTS of the instance, or the DTS of the formula set being processed.

Formulas do not need to be able to produce XBRL footnoteLink, footnoteArc, footnote, loc, schemaRef, roleRef, or arcRoleRef elements.

When the result of a formula contains a numeric item type, the unit element to which its unitRef attribute refers does not have to have an identifier unique among all unit elements in the output; the identifier of the unit element is unconstrained so long as the result output is XBRL-valid.

When the result of a formula contains a fact, the context element to which its contextRef element refers does not have to have an identifier unique among all context elements in the output; the identifier of the context element is unconstrained so long as the result output is XBRL-valid.

8.8 Result expressions may limit the precision of result numeric items

The default precision attribute of a numeric result is the maximum allowed by the input facts and the expression, but is truncated to 18 if a repeating decimal representation would result.

All numeric facts are asserted with a precision attribute unless decimals is specified.

8.9 Result expressions may limit the decimals of result numeric items

The default decimals attribute of the result is that which would result after conversion of all inputs to their equivalent precision attribute and requirement 8.8 adhered to and then converted back to a decimals attribute.

8.10 Result expressions may return Nil facts

That is, the result element would have xsi:nil="true".

8.11 Result expressions may construct derived tuples

Each formula may specify how new elements are to be constructed as a consequence of the presence and content of other facts in an instance. All parts of the result tuple MUST be specifiable by the formula, including element names, content of each element, context, and in the case of numeric facts, the unit and either decimals or precision attributes.

Example 34: Formula produces a tuple.

One example of the need to produce tuples as the output of formulas is when converting an instance using one taxonomy’s representation of some information, into the same information as represented in another taxonomy. In this example information is extracted from an instance whose taxonomy includes every asset class explicitly, and produce an instance whose taxonomy treats all asset classes as tuples distinguished by an IntangibleAssetClass child element; for example, for every occurrence of an item (IntangiblesPatents), i.e.,

<IntangibleGrossPatents

contextRef='c03' unitRef='usd' decimals='0'>10742</IntangibleGrossPatents>

Create a corresponding tuple:

<IntangiblesClass contextRef='c03'>patent</IntangiblesClass>

<IntangiblesGross

contextRef='c03' unitRef='usd' decimals='0'>10742</IntangiblesGross>

</IntangibleAsset>

Formulas:

tuple

test

expression

type

matching

"<IntangibleAsset>

<IntangiblesClass contextRef='{@contextRef}'> patent </IntangiblesClass>

</IntangibleAsset>"

$IntangiblesPatents

Tuple

p-equal,

u-equal and

c-equal;

The current node “.” Is bound to the fact (not its value).

Facts:

@id	item	@contextRef	@unitRef	decimals	[content]
f51	IntangiblesPatents	c03	usd	0	10742

Result:

@id	item	@contextRef	@unitRef	decimals	[content]
f52	IntangiblesClass	c03			Patent
f53	IntangiblesGross	c03	usd	0	10742
f54	IntangibleAssets				(tuple)

Example 35. Formula merges items into an existing tuple.

Continuing Example 34, the input and output taxonomies can differ by having several facts that need to be merged into an output tuple. Without the ability to merge into existing output tuples, a combinatorial number of formulas would be needed to capture each possible combination of facts available. For example, the additional facts appear in the input:

<IntangibleReservePatents

contextRef='c03' unitRef='usd' decimals='0'>3977</IntangiblesReservePatents>

<IntangibleNetPatents

contextRef='c03' unitRef='usd' decimals='0'>6765</IntangibleNetPatents>

This should yield, along with the inputs of use Example 34, a single tuple:

<IntangiblesClass contextRef='c03'>patent</IntangiblesClass>

<IntangiblesGross

contextRef='c03' unitRef='usd' decimals='0'>10742</IntangiblesGross>

<IntangiblesReserve

contextRef='c03' unitRef='usd' decimals='0'>3977</IntangiblesReserve>

<IntangiblesNet

contextRef='c03' unitRef='usd' decimals='0'>6765</IntangiblesNet>

</IntangibleAsset>

Formulas:

tuple

test

expression

type

matching

"<IntangibleAsset>

<IntangiblesClass contextRef='{@contextRef}'> patent </IntangiblesClass>

</IntangibleAsset>"

$IntangibleReservePatents

Merge the output tuple with any tuple already present having a duplicate IntangiblesClass element.

Tuple

p-equal,

u-equal and

c-equal;

The current node “.” Is bound to the fact (not its value).

"<IntangibleAsset>

<IntangiblesClass contextRef='{@contextRef}'> patent </IntangiblesClass>

</IntangibleAsset>"

$IntangibleNetPatents

Merge the output tuple with any tuple already present having a duplicate IntangiblesClass element.

Tuple

p-equal,

u-equal and

c-equal;

The current node “.” Is bound to the fact (not its value).

Input facts:

@id	item	@contextRef	@unitRef	decimals	[content]
f51	IntangiblesGrossPatents	c03	usd	0	10742
f52	IntangiblesReservePatents	c03	usd	0	3977
f53	IntangiblesNetPatents	c03	usd	0	6765

Result facts:

Merging a tuple into a null tuple yields the tuple itself. Formula processors may choose to implement tuple merging in a post-processing step. Merging into an output tuple does not by itself determine location in the output.

@id	item	@contextRef	@unitRef	decimals	[content]
f54	IntangiblesClass	c03			patent
f55	IntangiblesGross	c03	usd	0	10742
f56	IntangiblesReserve	c03	usd	0	3977
f57	IntangiblesNet	c03	usd	0	6765
f58	IntangibleAssets				(tuple)

8.12 Result expressions may indicate that a result element is to be inserted into last inserted tuple

Requirement 8.11 above implies that additional formulas may create items or other tuples that are meant to be children of a previously output tuple. The default behaviour is to append the result to the xbrl root element.

9 Approval requirements

The requirements here apply to formula specifications and the process for their approval.

A formula specification must provide a listing of the formula requirements that are satisfied, but need not satisfy all requirements nor all requirements of all four use cases.

9.1 A formula specification MUST depend only on finalised specifications with broad implementation experience

A working definition of “broad” implementation experience is “at least as many commercial implementations as XBRL itself.” The expression syntax used within the formula specification is covered by this requirement.

Figure 6. Expression requirements vs. W3C specifications.

Requirement	[XPATH]	[XPATH2]	[XQuery]
5.6, Expressions MAY include conditional expressions.	No	Yes	Yes
5.13. Functions MAY be named and expressions defined outside a formula and referenced in its expressions	No	No	Yes
Use case Error! Reference source not found. “Error! Reference source not found.” Requirement 5.10 says only “The behaviour of a formula processor MUST be defined in the case of an expression evaluation exception.”	No	No	No
6.2. Formulas MAY restrict the facts that they bind based on their context	No	Yes	Yes

WcH: It remains issue 34 whether XPATH 2.0 will be a finalised specification in an appropriate time frame.

9.2 Two formula processing implementations MUST produce semantically equivalent results on a conformance suite

A conformance suite will consist of sets of inputs and their expected outputs according to the formula specification. The conformance suite will exercise each feature of the formula specification. The ability to process these inputs and produce semantically equivalent outputs will be taken as evidence of a compliant formula processing implementation. Evidence of two separate and compliant formula processing implementations both having non-discriminatory licensing terms MUST be provided before the specification can be issued as a recommendation.

Figure 7. XBRL formulas conformance testing

9.3 A formula specification MUST NOT redefine any term defined in any specification upon which it depends

In particular, the term “duplicate” must retain its XBRL meaning {4.1}.

10 Proposed requirements

Proposed requirements and corresponding use cases that are not part of the official set of requirements and that have not been conclusively rejected are documented here. The “?” indicates that the use case or requirement has been proposed.

10.1 ? A formula binds to the PTVI of an instance, not to the instance

Beneficial consequences of processing the PTVI rather than the instance itself include:

· Formula expressions are NOT required to draw inferences from the existence of calculation or essence‑alias arcs discoverable from the instance.

· Fact-binding criteria are NOT required to infer precision or decimals attributes.

· A formula processor would have to be a superset of an XBRL processor as defined in the XBRL 2.1 Conformance Suite [CONF].

Issues include:

· The PTVI is NOT formally defined in the XBRL 2.1 Recommendation.

· The PTVI of an instance tends to be much larger in byte count than the instance itself.

· This requirement would require modification of requirement 6.7 above, “Formulas MUST only bind facts that are explicitly present in the input”

· The PTVI must be defined so as to be compatible with proposed requirement Error! Reference source not found., “Error! Reference source not found.”

WcH: This remains a proposed requirement because the PTVI specification is still a work in progress.

11 Rejected requirements

Some previously proposed examples and corresponding requirements are documented here. The “*” prefix indicates that the requirement is rejected.

11.1 * Formulas may bind facts in multiple XML instances

This would add generalised addressing of absolute and relative URLs to the fact binding expressions. Examples include:

· http://data.example.com/2003/10K.xbrl -- refers to a specific document

· http://data.example.com/2003/ -- refers to a set of documents?

· http://data.example.com CurrentAssets – refers to an element somewhere on the web site?

11.2 * Formulas form arcs from their input items to outputs and directed cycles in these arcs are prohibited.

Formulas already do have a certain kind of directed cycle, where there is a directed cycle from the Equity item to itself except for the fact that the period of the input and output do not overlap. The static analysis to detect cycles is sufficiently complex that it does not seem worthwhile to mandate. Moreover, it is believed that formulas such as z = f(z) + c is a legitimate example even though solving them may require iteration or other techniques.

11.3 * The maximum number of facts bound in a formula is fixed

The number of facts to be bound in a given formula is always fixed. Arguments bound in a formula may not be bound to a sequence of facts for execution. Formulas such as “the sum of all revenues for years before 2001” and “the sum of values of the children of the item” are not required. This would essentially require operations on vectors and matrices spanning any number of contexts, which in turn requires a definition of the “best” or “maximal” match in order to avoid a combinatorial explosion. For example, if argument X is defined in six periods, then the “moving average of X” must be defined with respect to a fixed number of periods anyway (2 periods? 3 periods?), and this can adequately be expressed using formulas with a fixed number of input arguments. By contrast, if X is “the sum of X for all child entities,” all could mean “all child entities for which X is known in each known period” or “all child entities for which X is known in all periods.”

11.4 * Conforming processors MUST allow a user agent to copy the input instance to the output, and the processing model MUST state that it is the default

This would have required that the output of a formula processor to be either an empty instance or a copy of the input instance, and force the processing model to allow the choice to be overridden. This was removed from the requirements since it has no impact on the syntax of formulas.

11.5 * Formulas MAY specify one or more alternative items or tuples as the possible result of expression evaluation

The results from a formula may select a subset of a finite set of possible element names (items) that depend on the input facts. This is requirement is supported by general requirement 3.6, “The representation of formulas should not require redundancy”. An example would be the formula “If revenue is less than expense then loss is expense minus revenue, otherwise profit is revenue minus expense”. Another example would be a formula computing either or both of a Boolean flag and a diagnostic error message. In both examples, to achieve the same effect using two separate formulas having the same variable bindings and tests would be redundant. This requirement is not meant to imply that the element name(s) in the output might be synthesised via an expression; the formula would still need to explicitly list the possible alternative items, with the expression selecting among them. (Note that the fact that FRTA 1.0 and rule 2.1.1 – supported by FRTA 1.0 example 1 – would forbid the use of both profit and loss items suggests that a better example is needed than the one used here – a moot point since the requirement is rejected).

11.6 * Conforming processors MUST default the units of a result by analysis of the input facts and expression

The units of the fact resulting from a result expression have a default which is determined by analysis of the expression; e.g., a/b yields units(a)/units(b); a+b yields unit(a) and throws an exception if units(a)<>units(b), etc.

An example would be identical to Error! Reference source not found. in terms of facts and results except that the formula itself would not specify that the output results are a currency amount per year.

11.7 * Formulas MAY specify the location of their result in the output instance

The output result is by default appended to the root xbrl element of the output, but a path may be specified where it is to be inserted. This is a stronger version of result requirement 8.12 above.

11.8 * Expressions may test for duplicate output facts and tuples before asserting a result

The most general form of this requirement would mean evaluating expressions that reference the output instance—realistically this would have to be restricted to specific circumstances such as testing whether the fact about to be inserted is already present.

12 Document history (non-normative)

Date	Editor	Remarks
2002-01-10	vun Kannon	Note posted on XBRL-SpecV2 group describes the design of the “Computational Linkbases” prototype by David vun Kannon and Yufei Wang of KPMG.
2002-01-25	Hamscher	First draft of “Augmented Computational Linkbases” which included both requirements and an alternate design proposal.
2002-02-18	Hamscher	Edits after draft reviewed by David vun Kannon.
2002-02-20	Hamscher	Draft distributed to the XBRL-SpecV2 group.
2002-02-27	Hamscher	Draft with inline edits by Geoff Shuetrim published to XBRL-SpecV2 group.
2002-07-01	Hamscher	Reissued as internal working draft of a Requirements document, with examples from Rene van Egmond added. The notion of a “rule base” is the functional requirement which might be satisfied by a computational linkbase with modifications.
2002-07-03	Hamscher	Issued as internal working draft to XBRL-SpecV2 group after comments by contributors.
2002-08-31	Hamscher	Incorporated comments on initial working draft. In recognition of issues illustrated in the draft specification of 2002-08-19, some requirements were reworded, dropped, or changed category.
2002-09-10	Hamscher	Incorporated further minor comments and requested issuance as a public working draft.
2002-09-25	Hamscher	Relaxed the requirement for an open source implementation, and relaxed the requirement with respect to XPATH 2.0. Changed intellectual property notices to conform to IPR policy currently pending ISC approval. Revised target approval dates. Requested again issuance as a public draft.
2002-09-26	Hamscher	Corrections in use cases and various typos caught by Watanabe-san. Added line numbering to facilitate commentary.
2002-10-01	Hamscher	Finalisation for public release. Removed redundant use case 5 and renumbered the remainder.
2002-10-16	Hamscher	Various errata from Hugh Wallis. Returned to previous numbering and stabilised on UC01, UC02, etc. Reinstated a simplified UC05.
2002-10-22	Hamscher	Various marginal notes included from New York face-to-face meeting 22 October 2002 which changed the status of some requirements from basic to complex and vice versa.
2003-11-14	Hamscher	Updated entire document contents to conform to XBRL 2.1 syntax and style. Defined the relationship between this new specification and XBRL 2.1. Removed the distinction between basic and complex requirements. Restated each requirement as a normative statement and defined conformance with stringency similar to that of XBRL 2.1. Included consideration of the impact of duplicates and other XBRL 2.1 issues. Eliminated the Open Issues and Design notes sections, folding any relevant remarks into the explanation for each requirement. Revised use cases to remove cases now irrelevant and added general scenarios of use.
2003-12-07	Hamscher	Incorporated feedback from Yuji Furusho, Geoff Shuetrim and others.
2004-01-08	Hamscher	Reworked the use cases to use a common set of concepts, contexts, and units. Reorganised document to emphasise concrete use cases. Broke requirements up into several separate sections by theme. Distributed a truncated draft for comments to the Formula subgroup.
2004-01-12	Hamscher	Brought draft into alignment with issues list. Referenced each individual requirement to a use case. Added additional use cases but left others open for others to add. Added sections of proposed and rejected requirements (and use cases). Indicated in the draft where outstanding decisions need to be made and provided notes on the issues.
2004-01-18	Hamscher	Promoted the proposed requirements for multiple formulas per item, and globally defined functions; added several new proposed requirements that emerged in online discussions. Added an approval requirement that terms must not be redefined. Added explicit requirement that expressions may produce tuples. Made editorial change to distinguish arguments and variables. Added use cases to clarify the treatment of units in output expressions. Updated target completion dates.
2004-02-02	Hamscher	Added explanation of general use cases and added proposed requirement relaxing the need for XBRL output.
2004-02-11	Hamscher	Rejected the requirement that each formula binds a fixed number of facts, replacing it with a use case involving summation across segments and the accompanying requirement that expressions must be able to access the DTS of the instance that it is processing. Merged David vun Kannon’s edits to expression syntax so as to use XPATH 2.0 W3C Working Draft 12 November 2003 syntax, and incorporated his observations into a table in the “broadly implemented expression language” requirement. Promoted the rejected requirement to have computed item results to a proposed requirement.
2004-02-16	Hamscher	Merged comments from Hugh Wallis to use s‑equal instead of “equivalent” or “same” contexts, and typographical errors in some use cases. Reworded the use case for formula prohibition to refer to sets of formulas rather than taxonomies. Moved “arbitrary XML output” from proposed to rejected. Added result requirement that formula must indicate whether result is a child of the xbrl element or the last tuple.
2004-03-17	Hamscher	Incorporated changes to rules so as to align the treatment of formulas from the standpoint of duplicates and archiving with the treatment of calculation arcs under XBRL 2.1. Edited the rule regarding prohibition. Corrected typos found by Mark Goodhand.
2004-04-06	Hamscher	Modified the segment summation use case to clarify that the formula fact matching over segments must take into account the meaning of the segment child elements, and conversely that the segment child elements should be designed so as to distinguish orthogonal segmentations. Clarified the rule regarding input copying so as to remove it from the realm of linkbase syntax. Promoted the requirement for accessibility of all parts of the input instance to a full requirement. Removed use case involving formula sequencing using roles. Rejected requirements concerning processing iterations, multiple alternative item outputs, computation of output units, and testing for duplicate outputs. Clarified that the output instance may have duplicate contexts and units, so long as the result is XBRL-valid.
2004-04-20	Hamscher	Edit to turn Internal WD into Public WD, no other changes.
2005-06-07	Hamscher	Reorganized individual use cases into examples to support requirements; layered the requirements into four generic use cases, and relaxed the requirement that the specification satisfy all requirements of all use cases. Updated reference list. Edit to turn PWD into Draft Candidate Recommendation.
2005-06-13	Hamscher	Typographical corrections.

13 Intellectual Property Status (non-normative)

This document and translations of it may be copied and furnished to others, and derivative works that comment on or otherwise explain it or assist in its implementation may be prepared, copied, published and distributed, in whole or in part, without restriction of any kind, provided that the above copyright notice and this paragraph are included on all such copies and derivative works. However, this document itself may not be modified in any way, such as by removing the copyright notice or references to XBRL International or XBRL organizations, except as required to translate it into languages other than English. Members of XBRL International agree to grant certain licenses under the XBRL International Intellectual Property Policy (www.xbrl.org/legal).

This document and the information contained herein is provided on an "AS IS" basis and XBRL INTERNATIONAL DISCLAIMS ALL WARRANTIES, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO ANY WARRANTY THAT THE USE OF THE INFORMATION HEREIN WILL NOT INFRINGE ANY RIGHTS OR ANY IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE.

The attention of users of this document is directed to the possibility that compliance with or adoption of XBRL International specifications may require use of an invention covered by patent rights. XBRL International shall not be responsible for identifying patents for which a license may be required by any XBRL International specification, or for conducting legal inquiries into the legal validity or scope of those patents that are brought to its attention. XBRL International specifications are prospective and advisory only. Prospective users are responsible for protecting themselves against liability for infringement of patents. XBRL International takes no position regarding the validity or scope of any intellectual property or other rights that might be claimed to pertain to the implementation or use of the technology described in this document or the extent to which any license under such rights might or might not be available; neither does it represent that it has made any effort to identify any such rights. Members of XBRL International agree to grant certain licenses under the XBRL International Intellectual Property Policy (www.xbrl.org/legal).

14 References (non-normative)

[CONF]	Walter Hamscher (editor).
	XBRL 2.1 Conformance Suite 1.0 Public Working Draft
	http://www.xbrl.org/

[FRTA]	Walter Hamscher (editor).
	Financial Reporting Taxonomy Architecture 1.0
	http://www.xbrl.org/

[HNC]	Fair Isaac & Company, Inc.
	Blaze Advisor
	http://www.fairisaac.com

[ISO]	International Standards Organisation.
	ISO 4217 Currency codes, ISO 639 Language codes, ISO 3166 Country codes, ISO 8601 international standard numeric date and time representations.
	http://www.iso.ch/

[ILOG]	JRules
	ILOG Inc.
	http://www.ilog.com/products/rules/engines/jrules/

[HPS]	Alan Newell and Herb Simon.
	Human Problem Solving, 1972.

[Processes]	Walter Hamscher
	XBRL International Processes 1.0, 4 April 2002
	http://www.xbrl.org/

[RFC2119]	Scott Bradner
	Key words for use in RFCs to Indicate Requirement Levels, March 1997
	http://www.ietf.org/rfc/rfc2119.txt

[SCHEMA‑0]	World Wide Web Consortium
	XML Schema Part 0: Primer.
	http://www.w3.org/TR/xmlschema-0/

[SCHEMA‑1]	World Wide Web Consortium
	XML Schema Part 1: Structures
	http://www.w3.org/TR/xmlschema-1/

[SCHEMA‑2]	World Wide Web Consortium
	XML Schema Part 2: Datatypes
	http://www.w3.org/TR/xmlschema-2/

[XBRL]	Phillip Engel, Walter Hamscher, Geoff Shuetrim, David vun Kannon and Hugh Wallis
	Extensible Business Reporting Language 2.1 Recommendation, with corrected errata to 2005-04-25
	http://www.xbrl.org/TR/2003/XBRL-Recommendation-2003-12-31.doc

[XLink]	Steve DeRose, Eve Maler, and David Orchard
	XML Linking Language (XLink) Version 1.0
	http://www.w3.org/TR/xlink/

[XML]	Tim Bray, Jean Paoli, and C.M. Sperberg-McQueen
	Extensible Markup Language (XML) 1.0 (Second Edition)
	http://www.w3.org/TR/rec-xml

[XPATH]	James Clark and Steve DeRose
	XML Path Language (XPath) 1.0 Specification
	http://www.w3.org/TR/xpath/

[XPATH2]	Andreas Berglund et al., editors.
	XML Path Language (XPath) 2.0
	W3C Working Draft 4 April 2005
	http://www.w3.org/TR/xpath20/

[XQPFO]	Ashok Malhotra, Jim Melton and Norman Walsh
	XQuery 1.0 and XPath 2.0 Functions and Operators
	W3C Last Call Working Draft 12 November 2003
	http://www.w3.org/TR/xpath-functions/

[XQuery]	Scott Boag et al., editors.
	XQuery 1.0: An XML Query Language
	W3C Last Call Working Draft 12 November 2003
	http://www.w3.org/TR/xquery/

[XSLT]	Michael Kay
	XML Schema Transformation Language 2.0
	W3C Last Call Working Draft 12 November 2003
	http://www.w3.org/TR/xslt20/

[1] “type” here means either the result type if non numeric, or else the value of the precision or decimals attribute when the result is numeric.

Name	Contact	Affiliation
Walter Hamscher	walter@hamscher.com	Standard Advantage / Consultant to PricewaterhouseCoopers

Geoff Shuetrim	gshuetrim@kpmg.com.au	KPMG LLP
David vun Kannon	dvunkannon@kpmg.com	KPMG LLP

	Stage (* - Current)	Party responsible for decision	Next step	Revisions needed	Target date for stage completion
1	Internal WD	WG	Recommend for Stage 2	Stay in Stage 1	2004-01-27
2	Internal WD pending publication	ISC	Approve for Stage 3	Return to Stage 1	2004-02-25
3	Public WD under 45 day review	WD Editor(s)	Minor revisions – to Stage 4	Major revisions, Restart Stage 1	2004-04-20
4	Public WD pending publication	WG	Recommend for Stage 5	Restart Stage 3	2005-06-21
5	* Candidate Recommendation	ISC	Approve for Stage 6	Restart Stage 4	2005-07-19
6	Recommendation	Done

Editors

Status of this document

Table of contents

1 Motivation (non-normative)

1.1 Terminology and formatting conventions

1.2 Normative status

1.3 Language independence

2 Use cases

3 Linkbase-related requirements

3.1 A discoverable taxonomy set may include formulas

3.2 Formulas may require components of a DTS

3.3 Formulas may be partitioned into sets

3.4 Formulas MAY be prohibited

3.5 Documentation of a formula may be included

3.6 The representation of formulas should not require redundancy

3.7 Formulas must only appear in linkbases associated with a taxonomy, consistent with the treatment of calculations, and not the instance.

4.2 Application of a set of formulas to an XBRL-valid instance MUST either fail or result in a well-formed XML instance.

4.3 Application of a set of formulas to an XBRL-valid instance MUST either fail or result in another XBRL-valid instance.

4.4 Any number of formulas may compute the value of any item.

4.5 All formulas in a DTS must be processed concurrently and without exception without regard to priority.

5.1 There MUST be only one expression language

5.2 The expression language MUST be recognisable to a programmer of average skill.

5.3 The expression language MUST include operators that can select any node in the instance accessible from bound facts.

5.4 Expressions may include constants.

5.5 Expressions MAY include mathematical operations.

5.7 Expressions MAY determine the minimum and maximum period that appear among the contexts in an instance.

5.8 Expressions may test for the presence of a fact for any concept in any context.

5.9 All facts must be bound before an expression is evaluated.

5.11 Constants MAY be named and defined inside a formula and referenced in its expressions.

5.12 Constants may be named and defined outside a formula and referenced in its expressions.

5.14 Functions MAY have their scope defined to apply to only a subset of formulas in a set

5.15 Expression evaluation exceptions MAY be caught to produce a result

6 Fact-binding Requirements

6.1 Formulas MAY filter the input facts to which they apply according to relationships between facts in one or more contexts.

6.6 Formulas MAY filter input facts based on the filters applied in that formula to other facts

6.8 Formulas MAY specify preconditions on expressions based on context and fact value

6.9 Formulas MAY bind facts that are present in more than one XBRL instance within a single root XML element

6.10 Multiple applications of a formula to a set of facts, with multiple combinations of bindings of arguments to facts, may produce multiple results

6.11 Formula bindings and behaviour MUST be defined in situations in which duplicates appear in the input instance

6.13 Constants MAY be facts

6.14 A variable number of facts may be bound

8 Result Expression Requirements

8.1 If the application of a formula results in an item then the formula must fully determine the context of that item

8.2 If the application of a formula results in a numeric item, then the formula processor must also result in a unit reference and a precision or decimals attribute

8.3 Formulas MAY include expressions to construct a derived item

8.4 Formulas MAY include expressions to construct a derived context

8.5 Formulas MAY include expressions to construct a derived unit

8.6 Formulas MAY create the content of a new item

8.7 A formula MUST be able to create contexts, units, and items that were not present in the input document

8.8 Result expressions may limit the precision of result numeric items

8.9 Result expressions may limit the decimals of result numeric items

8.10 Result expressions may return Nil facts

8.11 Result expressions may construct derived tuples

8.12 Result expressions may indicate that a result element is to be inserted into last inserted tuple

9.2 Two formula processing implementations MUST produce semantically equivalent results on a conformance suite

9.3 A formula specification MUST NOT redefine any term defined in any specification upon which it depends

10.1 ? A formula binds to the PTVI of an instance, not to the instance

11.1 * Formulas may bind facts in multiple XML instances

11.2 * Formulas form arcs from their input items to outputs and directed cycles in these arcs are prohibited.

11.4 * Conforming processors MUST allow a user agent to copy the input instance to the output, and the processing model MUST state that it is the default

11.6 * Conforming processors MUST default the units of a result by analysis of the input facts and expression

11.7 * Formulas MAY specify the location of their result in the output instance

11.8 * Expressions may test for duplicate output facts and tuples before asserting a result

12 Document history (non-normative)

13 Intellectual Property Status (non-normative)

14 References (non-normative)